The eponymous post, part 2

When whales are born on Tuesdays

In part 1, I explored the problem:

1. 'There are two whales. You are told that one of the whales is male. What is the probability that both whales are male?'

In part 2, I'll look at a slightly harder version of that puzzle:

2. 'There are two whales. You are told that one of the whales is male and was born on a Tuesday. What is the probability that both whales are male?'

In addition to the assumptions given in part 1, you may assume that the weekdays whales are born on are random, independent of each other, and independent of the sexes of the whales.

From part 1, we learned that the answer to 1) is 1/3 and, at first, one would be tempted to choose the exact same answer for 2). After all, what could the weekday a whale was born on have to do with their sex?

However, that answer is incomplete for the same reason that the erroneous answer to part 1 was: we are inadvertently making assumptions about which sets of possibilities our questions rule out. Last time we forgot that there are two ways for one whale to be male, and one whale to be female (MF and FM). This time, we are forgetting that there are two ways to make Male Tuesday (MT) whales.

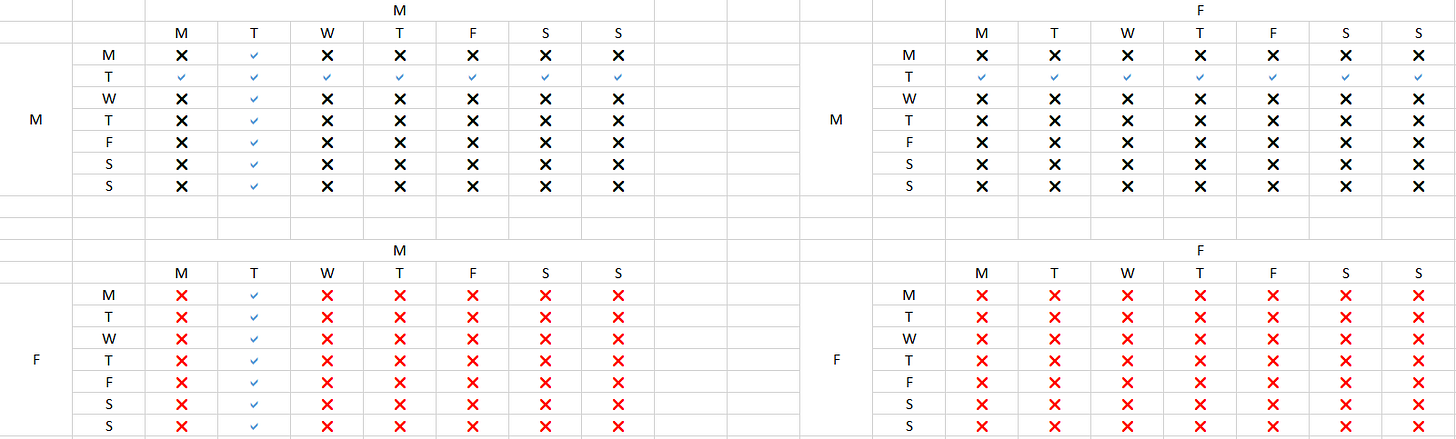
This table shows the possible combinations of sexes and weekdays of birth. As in part 1, we can cross out all the options in the FF table, but we also get to cross out all the options where there is not at least one MT whale. Crucially, the MM table shows that either the first, the second, or both whales could be MT whales. This actually makes the amount of possible MM combinations 2*7-1, which is nearly as many combinations as exist in the MF and FM tables. The final answer is 13/27.

In short, because there are two ways for the MM table to meet our restrictions, and only one way for each of the MF and FM tables can do so, the MM table ends up composing more of our possible worlds. One can observe that as the number of weekdays tends to infinity, the probability of MM tends to 1/2.

Side-note: In solving this problem, I assumed that, after these restrictions are applied, each one of the remaining possible worlds is equally likely. Why this is true is something I don't have entirely well formalized in my mind, so I would appreciate input on this specific point.